Angular Displacement Formulas og Løste Øvelser
den vinkelforskyvning Den genereres når et objekt beveger seg etter en bane eller bane som har form av en sirkel. Det er forskjellig fra forskyvningen; mens vinkelforskyvningen måler vinkelen som er reist, måler forskyvningen avstanden.
For å beregne vinkelforskyvningen av et objekt som beveger seg langs en omkrets, kan to måter brukes: Hvis den innledende og endelige vinkelen er kjent, vil vinkelforskyvningen være subtraksjonen mellom den endelige vinkelen og den innledende vinkelen.
Hvis lengden på forskyvningen (lengden av omkretsbue reist) og radius av omkretsen er kjent, blir vinkelforskyvningen gitt av θ = l / r.
index
- 1 formler
- 2 øvelser
- 2.1 Første øvelse
- 2.2 Andre øvelser
- 2.3 Tredje øvelse
- 3 referanser
formler
For å få formlene beskrevet ovenfor kan du se følgende bilder:
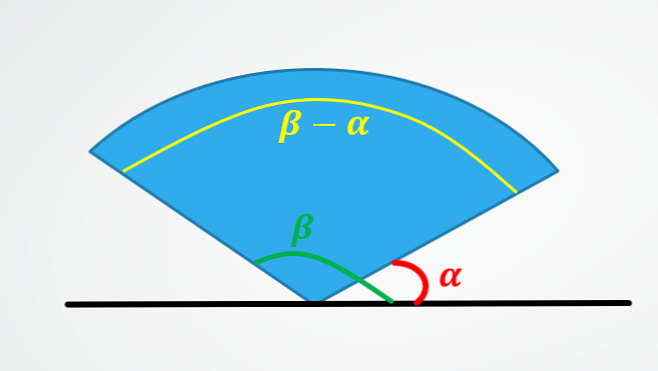
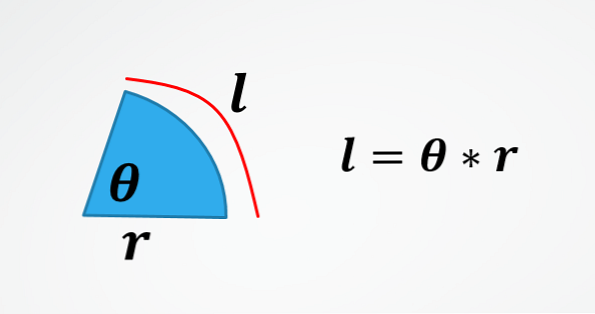
Den første viser hvorfor vinkelforskyvningen er lik subtraksjonen av den endelige vinkelen minus innledningsvinkelen.
I det andre bildet er formelen for lengden av en bue i en sirkel. Derfor, ved å rydde θ får du formelen beskrevet i begynnelsen.
trening
Nedenfor er noen øvelser hvor definisjonen av vinkelforskyvning skal anvendes og hvor formlene beskrevet ovenfor er brukt.
Første øvelse
Juan har kjørt en avstand på 35 meter på et sirkulært løpebane hvis radius er lik 7 meter. Beregn vinkelforskjellen som Juan har laget.
oppløsning
Siden avstanden til buen reiste og radiusen av omkretsen er kjent, kan den andre formel anvendes for å kjenne den vinkelforskyvning som er gjort av Juan. Ved å bruke formelen beskrevet ovenfor har du det θ = 35/7 = 5 radianer.
Andre øvelse
Hvis du har at Mario har reist i kjøretøyets halvdel av et sirkulært løpsspor, hva er vinkelforskyvningen som Mario har gjort??
oppløsning
I denne øvelsen vil den første formelen bli brukt. Siden det er kjent at Mario har reist halvparten av banen, kan det antas at han startet løpet i 0 ° vinkelen, og når han nådde midten av sirkelen, har han reist 180 °. Derfor er svaret 180 ° -0 ° = 180 ° = π radianer.
Tredje øvelsen
María har et sirkulært basseng. Hunden din løper rundt bassenget som dekker en avstand på 18 meter. Hvis radiusen til bassenget er 3 meter, hva er vinkelforskyvningen som er gjort av Marias maskot??
oppløsning
Siden bassenget er sirkulært og du vet radiusen av det, kan du fortsette å bruke den andre formelen.
Det er kjent at radiusen er lik 3 meter, og avstanden som kjøres av kjæledyret, er lik 18 meter. Derfor utføres vinkelforskyvningen som er θ = 18/3 = 6 radianer.
referanser
- Basto, J.R. (2014). Matematikk 3: Grunnleggende analytisk geometri. Patria Editorial Group.
- Billstein, R., Libeskind, S., og Lott, J. W. (2013). Matematikk: en problemløsende tilnærming til grunnlærerutdanning. López Mateos Editores.
- Bult, B., & Hobbs, D. (2001). Matematisk leksikon (illustrert utgave). (F. P. Cadena, Trad.) Utgave AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Math. Geometri. Reform av den øvre syklusen til E.G.B. Utdanningsdepartementet.
- Schneider, W., & Sappert, D. (1990). Praktisk teknisk tegnehåndbok: Introduksjon til det grunnleggende innen industriell teknisk tegning. Reverte.
- Thomas, G. B., & Weir, M. D. (2006). Beregning: flere variabler. Pearson Education.


