Broglie Atomic Model Egenskaper og Begrensninger

den Broglie atommodell ble foreslått av den franske fysikeren Louis Broglie i 1924. I doktorgradsoppgaven hevdet Broglie bølgenpartikkelenes dualitet av elektroner som legger grunnlaget for bølgemekanikk. Broglie publiserte viktige teoretiske funn om bølgekorpsulets natur i atomskalaen.

Deretter ble Broglie-uttalelsene eksperimentelt demonstrert av forskerne Clinton Davisson og Lester Germer, i 1927. Broglie-elektronbølgeteorien er basert på Einsteins forslag om lysets bølgelegenskaper ved korte bølgelengder.

Broglie kunngjorde muligheten for at saken hadde en oppførsel som lignet lys og foreslo lignende egenskaper i subatomære partikler som elektroner.

Elektriske ladninger og baner begrenser amplitude, lengde og frekvens av bølgen beskrevet av elektroner. Broglie forklarte bevegelsen av elektroner rundt atomkjernen.

index

• 1 Kjennetegn ved Broglie-atommodellen
• 2 Davisson og Germer eksperiment
• 3 begrensninger
• 4 Artikler av interesse
• 5 referanser

Kjennetegn ved Broglie-atommodellen

For å utvikle sitt forslag startet Broglie fra prinsippet om at elektroner hadde en dobbelt natur mellom bølge og partikkel, lik lys.

På denne måten gjorde Broglie en sammenligning mellom begge fenomenene, og basert på likningene utviklet av Einstein for studiet av lysets bølgeform, indikerte han følgende:

- Den totale energien til fotonet og følgelig den totale energien til elektronen, kommer fra produktet av frekvensen av bølgen og Plank-konstanten (6.62606957 (29) × 10 ^-34 Jules x sekunder), som beskrevet i følgende uttrykk:

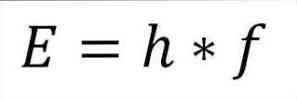
I dette uttrykket:

E = elektronenergi.

h = Plank konstant.

f = frekvens av bølgen.

- Det elektroniske lineære øyeblikket, og dermed av elektronen, er omvendt proporsjonalt med bølgelengden, og begge størrelser er relatert gjennom Plank-konstanten:

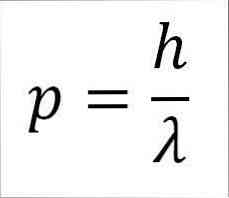
I dette uttrykket:

p = lineært øyeblikk av elektronen.

h = Plank konstant.

λ = bølgelengde.

- Det lineære momentum er produktet av massen av partikkelen med den hastigheten partikkelen har under dens forskyvning.

Hvis det forrige matematiske uttrykket er omstrukturert som en funksjon av bølgelengden, har vi følgende:

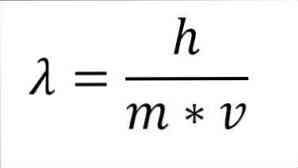
I nevnte uttrykk:

λ = bølgelengde.

h = Plank konstant.

m = massen av elektronen.

v = elektronhastighet.

Siden h, Plank-konstanten, har en liten verdi, er bølgelengden λ også. Følgelig er det mulig å angi at bølgenegenskapene til elektronen forekommer bare på atom- og subatomære nivåer.

- Broglie er også basert på postulatene av Bohrs atommodell. I følge sistnevnte er båndene til elektronene begrensede og kan bare være flere ganger av heltall. slik:

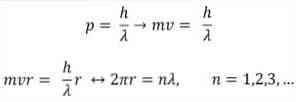
der:

λ = bølgelengde.

h = Plank konstant.

m = massen av elektronen.

v = elektronhastighet.

r = baneens radius.

n = hele tall.

Ifølge Bohr-atommodellen, som Broglie antok som grunnlag, hvis elektronene oppfører seg som stående bølger, er de eneste tillatte bane de som har en radius som er lik et integrert flertall av bølgelengden A.

Derfor oppfyller ikke alle bane parametrene som er nødvendige for at et elektron skal bevege seg gjennom dem. Derfor kan elektronene bare reise i bestemte baner.

Broglie-elektronernes bølgeteori begrunnede suksessen til Bohr-atommodellen for å forklare oppførselen til hydrogenatomerens eneste elektron.

Analogt ble det også lagt merke til hvorfor denne modellen ikke passet mer komplekse systemer, det vil si atomer med mer enn en elektron.

Davisson og Germer eksperiment

Den eksperimentelle verifikasjonen av Broglie-atommodellen fant sted 3 år etter utgivelsen, i 1927.

De fremtredende amerikanske fysikerne Clinton J. Davisson og Lester Germer eksperimentelt bekreftet teorien om bølgemekanikk.

Davisson og Germer utførte spredningstester av en elektronstråle gjennom en nikkelkrystall og observert diffraksjonsfenomenet gjennom metallmediet.

Forsøket utført besto av å utføre følgende fremgangsmåte:

- I første omgang ble en samling med elektronstråle plassert som hadde en kjent startenergi.

- En spenningskilde ble installert for å akselerere bevegelsen av elektroner, noe som førte til en potensiell forskjell.

- Strømmen av elektronstrålen ble rettet mot en metallisk krystall; i dette tilfellet nikkel.

- Antallet elektroner som påvirket nikkelkrystallen ble målt.

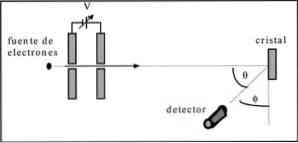
På slutten av forsøket oppdaget Davisson og Germer at elektronene ble spredt i forskjellige retninger.

Ved å gjenta forsøket ved å bruke metallkrystaller med forskjellige orienteringer, oppdaget forskerne følgende:

- Spredningen av elektronstrålen gjennom metallkrystallen var sammenlignbar med fenomenet interferens og diffraksjon av lysstrålene.

- Refleksjonen av elektronene på effektkrystallet beskrev banen som, teoretisk sett, skulle beskrive i henhold til teorien om elektronbølger av Broglie.

I syntesen viste eksperimentet av Davisson og Germer eksperimentelt den elektroniske dobbeltbølge-partikkel-naturen.

begrensninger

Broglie-atommodellen forutsier ikke nøyaktig plasseringen av elektronen på bane hvor den beveger seg.

I denne modellen blir elektroner oppfattet som bølger som beveger seg rundt bane uten en bestemt plassering, som introduserer begrepet elektronisk bane.

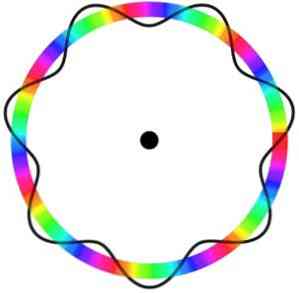
I tillegg vurderer Broglie-atommodellen, som er analog med Schrödinger-modellen, ikke rotasjonen av elektroner på sin akse (spin).

Ved å ignorere det indre vinkelmomentet for elektroner blir de romlige variasjonene av disse subatomære partikler forsømt..

I samme rekkefølge av ideer tar denne modellen ikke hensyn til endringer i oppførselen til raske elektroner som følge av relativistiske effekter.

Artikler av interesse

Atommodell av Schrödinger.

Atommodell av Chadwick.

Atommodell av Heisenberg.

Atommodell av Perrin.

Atommodell av Thomson.

Atommodell av Dalton.

Atomisk modell av Dirac Jordan.

Atomisk modell av Democritus.

Atommodell av Bohr.

referanser

1. Bohrs Quantum Theory og De Broglie Waves (s.f.). Hentet fra: ne.phys.kyushu-u.ac.j
2. Louis de Broglie - Biografisk (1929). © Nobelfondet. Hentet fra: nobelprize.org
3. Louis-Victor de Broglie (s.f.). Hentet fra: chemed.chem.purdue.edu
4. Lovett, B. (1998). Louis de Broglie. Encyclopædia Britannica, Inc. Hentet fra: britannica.com
5. Atomisk modell av De Broglie. National University of Distance Education. Spania. Hentet fra: ocw.innova.uned.es
6. Waves Of Matter Of Louis De Broglie (s.f.). Hentet fra: hiru.eus
7. Von Pamel, O., og Marchisio, S. (s.f.). Kvantemekanikk National University of Rosario. Hentet fra: fceia.unr.edu.ar